LEYES DE LOS LIMITES
Usamos las siguientes propiedades de límites, llamadas
Leyes de Límites, para calcular límites.
Estas cinco leyes se pueden expresar verbalmente como
sigue:
1. El límite de la
suma de límites es la suma de los límites.
2. El límite de
una diferencia es la diferencia de los límites.
3. El límite de
una constante por una función es la constante por el límite de la función.
4. El límite de un
producto es el producto de los límites.
5. El límite de un
cociente es el cociente de los límites (siempre que el límite del de- nominador
no sea 0).
Es fácil creer que estas propiedades son verdaderas. Por
ejemplo, si f (x) es cercana a L y
g (x) es cercana a M, es
razonable concluir que f (x) + g(x)
es cercana a L + M. Esto nos da una
base intuitiva para pensar que la Ley 1 es verdadera.
Si usamos la Ley 4 (Límite de un Producto) repetidamente
con g(x) = f (x), obtenemos la
siguiente Ley 6 para el límite de una potencia. Una ley similar se cumple para
raíces.
En palabras, estas leyes dicen lo siguiente:
6. El límite de una potencia es la potencia del límite.
7. El límite de una raíz es la raíz del límite.
EJEMPLO 1 Uso de las leyes de límites
Use las leyes de límites y las gráficas de f y g en la Figura 1 para evaluar los
siguientes límites si existen.
(a) De las gráficas f
y g vemos que:
Por lo tanto tenemos
(b) Vemos que
no existe porque los límites izquierdo y
derecho son diferentes:
Entonces no podemos usar la Ley 4 (Límite de un
Producto). El límite dado no existe, porque el límite izquierdo no es igual a
límite derecho.
(c) Las gráficas muestran que:
Como
el límite de un denominador es 0, no podemos usar la Ley 5 (Límite de un
Cociente). El límite dado no existe porque el denominador se aproxima a 0
mientras que el numerador se aproxima a un número diferente de cero.
Aplicación de las leyes de los limites
Al aplicar las Leyes de Límites, necesitamos usar cuatro
límites especiales
Los Límites Especiales 1 y 2 son intuitivamente obvios;
viendo las gráficas de y = c y y = x nos convencerá de su validez. Los
Límites 3 y 4 son casos especiales de las Leyes de Límites 6 y 7 (Límites de
una Potencia y una Raíz).
EJEMPLO 2 Uso de las Leyes de Límites
Evalúe los límites siguientes, y justifique cada paso.
(b) Empezamos por usar la Ley 5, pero su uso está
totalmente justificado sólo en la etapa final cuando vemos que existen los
límites del numerador y denominador y el límite del denominador no es 0.





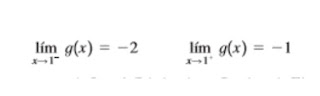






De que libro sacaste la información de los cuadros color celeste.
ResponderEliminarStewart 6 Edición
ResponderEliminarStewart 6 Edición
ResponderEliminarBuenas tardes. Cómo se calcula el límite de lim x_0 (1+ax) elevado a 1/x, cuando x tiende a cero. Gracias
ResponderEliminar