1 MÉTODO DE SUMA Y RESTA
PASO A PASO CONTESTAMOS
Sistema de ecuaciones
| 3x-7=y | . . . . . . . . . (1) |
| 4x-5y=2 | . . . . . . . . . (2) |
Procedimiento
- Ordenamos las ecuaciones para que los términos semejantes queden en la misma columna.3x-7=y . . . . . . . . . . (1)
3x-y=7 - Multiplicamos una de las ecuaciones para que el coeficiente de una de las variables sea igual en ambas ecuaciones.5(3x – y= 7)
15x – 5y =35 . . . . . . . . . . (3) - Eliminamos la incógnita cuyos coeficientes son iguales, por medio de una resta.
15x – 5y =35. . . . . . . . . . (3) -4x – 5y =2 . . . . . . . . . . (2) 11x =33 - Resolver la ecuación que resulta, para encontrar el valor de "x".11x = 33 . . . . . . . . . . (4)
x= 33/11
x = 3 - Sustituimos el valor de "x" en una de las ecuaciones iniciales para encontrar el valor de "y"3x – 7 = y
3(3) -7 =y
9-7= y
2=y - Comprobamos los valores encontrados para "x" y "y" , sustituyéndolos en las ecuaciones (1) y (2).3x – 7 = y . . . . . . . . . .(1)
3(3) -7 =y
9-7= y
2=y
4x – 5y =2 . . . . . . . . . . (2)
4(3) -5(2) = 2
12-10=2
2=2
Método de Igualación paso a paso
Básicamente, el método de igualación consiste en:
- Despejar una incógnita en una de las ecuaciones, que quedará en función de la otra incógnita (seguiremos teniendo una ecuación).
- Despejar la misma incógnita en la otra ecuación
- Igualar los segundos miembros de las dos incógnitas despejadas, formando una nueva ecuación con una incógnita.
- Despejar la única incógnita que nos quede. Obtenemos el valor numérico de una incógnita.
- Sustituir la incógnita despejada en el paso 4 por su valor numérico en cualquiera de las dos ecuaciones originales
- Operar para obtener el valor numérico de la otra incógnita.
Vamos a verlo más despacio el método de igualación con un ejercicio resuelto paso a paso.
Vamos a resolver por ejemplo el siguiente sistema de ecuaciones:
Para saber en todo momento a qué ecuación del sistema nos referimos, a la ecuación de arriba le llamaremos primera ecuación y a la de abajo segunda ecuación:
1- Despejamos una incógnita en una de las ecuaciones, teniendo en cuenta las reglas de la transposición de términos.
La más fácil para despejar es la “y” en la primera ecuación, ya que no tiene ningún número delante y además tiene un signo más delante, por lo que tan sólo pasando el 5x al otro lado ya tenemos la y despejada:
2- Despejamos la misma incógnita en la segunda ecuación:
3- Igualamos los segundos miembros de las incógnitas despejadas en los pasos 1 y 2:
4- Ahora tenemos una ecuación que depende sólo de x. Si necesitas ayuda con las ecuaciones de primer grado, dentro de mis cursos, puedes encontrar el Curso de Ecuaciones de Primer Grado, donde explico muy detalladamente cómo resolver ecuaciones de primer grado, con ejercicios resueltos paso a paso y propuestos para practicar con la solución.
La despejamos:
5- Este valor lo sustituimos por ejemplo en la primera ecuación:
6- Y operamos para obtener el valor de y:
Por tanto, la solución de este sistema es x=2, y=-2.
MÉTODO DE DETERMINANTES.
METODO DE DETERMINACION O METODO CRAMER:
Siempre empezamos enumerando las ecuaciones, el método cramer nos pide encontrar tres determinantes:
- determinante del sistema ∆S
- determinante de la x ∆X
- determinante de la y ∆Y
La forma de encontrar las determinantes es muy sencilla, de hecho este método es de mayor preferencia por los estudiantes, ya que solo se debe multiplicar para encontrar el valor de las incógnitas, pero para poder hacer este método siempre la ecuación debe tener Termino de x termino de Y, termino independiente
Aquí una breve explicación de este método:
Para encontrar el determinante del sistema, ósea de las dos ecuaciones, debemos colocar los coeficientes de las letras X & Y, y multiplicarlos de la siguiente manera:
Después de reacomodar los coeficientes de las variables. El paso a seguir es multiplicar los coeficientes en diagonal, restando después los productos de cada uno de ellos
como resultado tenemos que el determinante del sistema es 29
Para hallar el determinante de X hacemos un procedimiento similar, con la única diferencia que en lugar de colocar los coeficientes de X ponemos los términos independientes de cada ecuación
El ultimo determinante por hallar es el Y, Como el ultimo procedimiento lo único que cambia es que donde debería ir los coeficientes de Y, colocamos los términos independientes de cada ecuación
Después de hallar los determinantes, lo ultimo por hacer es encontrar los valores de las incógnitas X y Y.
Todo lo que hicimos fue tomar el determinante de X y dividirlo por el determinante del Sistema
Para hallar la incógnita de Y, tomamos el determinante de Y, dividiéndolo por el determinante del sistema.
R/= (-2, -4 )
MÉTODO DE FORMULA GENERAL
Fórmula general de ecuaciones de segundo grado completas.
Una vez identificadas las constantes, para resolver las ecuaciones de segundo grado completas hay que aplicar la siguiente fórmula:
Vamos a ver como se utiliza, resolviendo los ejemplos anteriores:
Tenemos la primera ecuación de segundo grado, en la que hemos identificado las constantes:
Ahora, tenemos que sustituir el valor de cada constate en la fórmula general:
Y ahora operamos, dentro de la raíz, teniendo en cuenta la jerarquía de operaciones:
Llegados a este punto, tenemos que resolver por un lado el signo + y por el otro el signo – :
Luego las dos soluciones sería -1 y -4. Si tuviéramos el caso de que las fracciones no fueran exactas, habría que simplificarlas.
Mucho cuidado con los signos – de las constantes. En el curso de cómo resolver ecuaciones de segundo grado, explico más detalladamente cómo resolver paso a paso cuando se nos presenta este caso. Es una de las causas de que no llegar al resultado correcto.
Existen casos particulares donde el resultado de la raíz es negativo, o que sus soluciones no son exactas o bien el resultado de la raíz no es exacto.
EJERCICIOS PROPUESTOS EN ESTOS LINK
REVISA EL SIGUIENTE VÍDEO PARA QUE REFORSAR TUS CONOCIMIENTOS
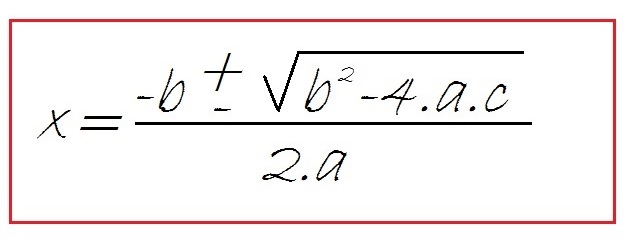
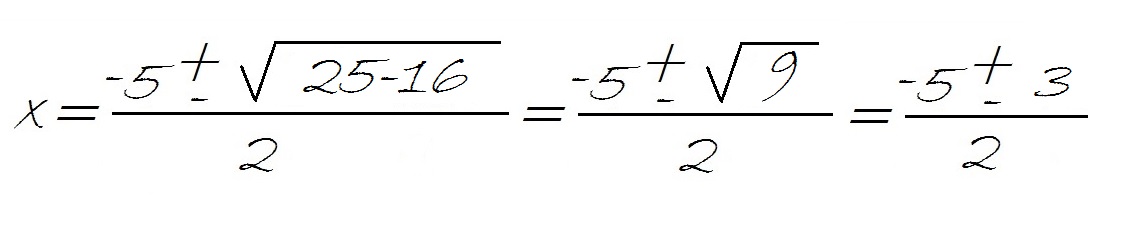
No hay comentarios:
Publicar un comentario